Sequence labeling and HMM part 2
HMM의 세 가지 기본 문제
- 1960년대 IDA의 잭 퍼거슨
- 문제 1 : (평가) 주어진 관찰 순서. observation 시퀀스(input 시퀀스)가 나타났을 때 주어진 HMM모델 람다=A,B (A : transition probability matrix, B : observation probability matrix) 하에서 이러한 (O=O1O2…OT)인풋 시퀀스가 나타날 확률
⇒ 확률 값이 낮으면 잘못된 시퀀스이다. 결국 이 시퀀스가 맞느냐 안맞느냐는 확률 값으로 판단이 가능할 것. 만약 이 문제가 음성인식이라면, 인식해 낸 시퀀스가 여러 개 있을 때 시퀀스 확률 값이 높은 것을 선택하는 것이 맞겠죠. 더 그럴듯한 시퀀스니까 음성인식의 경우 시그날(음파)이 input이고, 문장이 출력이다. 음파의 시그날을 가지고 여러개의 타겟문장이 나타난다. 각각에 대한 시퀀스 확률을 계산해 내면 제일 높은 시퀀스를 선택한다.
- 문제 2 : (디코딩) 아이스크림 문제의 숫자열이 나타났을 때 날씨 열을 찾는 것. 그것을 디코딩이라고 한다. 즉, observation sequence가 나타났을 때, 그리고 우리가 HMM 모델을 만들었을 때, 이 observation열에 맞는 (가장 적합한) 상태 시퀀스 (날씨의 경우 HOT, COLD 등)
- 문제 3 : (학습) 확률값은 어떻게 계산하는가? observation 데이터를 가장 잘 설명하는 람다를 찾아내는 것. 모델을 학습하는 것
문제 1 : 관측값 계산
- 학습된 모델이 아래와 같다고 가정

O = 3 1 3 일 확률을 계산해보자
- 가능성을 계산하는 법
- Markov 체인의 경우, 상태 3 1 3을 따라확률을 곱한다.
- 그러나 HMM의 경우 상태가 무엇인지 모른다. 3이 뭐고 1이 뭔지 어케 아는가?
- HCH = 0.8 * 0.3 * 0.4 … 이런식으로 H가 3이될 확률, C가 1이 될 확률, H가 3이 될 확률을 곱해줘야 한다.
- Hidden state : 우리가 원하는 것 = H와 C를 찾는 것. 품사 태깅으로 하면 품사 개수를 아는 것 (앗 46개다!) 46개의 hidden state가 있을 때, 4개의 단어로 이루어진 문장은 observation 4라는 것이다. (464)⇒ N개의 hidden state와 T개의 관측값 시퀀스가 있는 HMM의 경우 → NT
- 따라서 각 hidden state 시퀀스에 대해 별도의 계산을 할 수 없다.
- Forward 알고리즘
- 동적 프로그래밍 연산. CKY 파싱처럼. 테이블을 사용하여 중간 값 저장
- 아이디어 : 가능한 모든 hidden state 시퀀스를 합산하여 observation 시퀀스의 가능성을 계산한다.
⇒ 모든 가능한 상태로 계산해 가면서 값을 차곡차곡 채워들어가면 된다. 나중에 모든 가능한 상태 값을 계산하여 더한다. - 마지막 상태가 되는 확률값을 찾아낸다. 다양한 상태로 나타나는 확률을 다 더해준다. = at(j)를 찾는 것
- 알파 t의 j값을 찾는 것이다. 주어진 시퀀스(t개의 시퀀스)가 왔을 때, j번째 인풋 단어가 t번째 상태가 되는 확률. 품사라면 46개의 품사 중 1번서부터 46번까지 번호를 매겼을 때, qt라는 것은 ot에 해당하는 상태가 j번째 상태가 되는 확률을 얘기하는 것이다. 이것을 구하는 것을 포워드 알고리즘이라고 한다.

forward Recursion
- Initialization : 알파1(j) = a0jbj(o1)
start 상태에서 각각의 j는q1에서부터 q46 (품사라고 할때)
- Recursion : 각각을 계산해서 더해준다. 각각이 start state인 것 처럼
- Termination : 마지막으로 다 합쳐주면 우리가 원하는 확률 값이 나온다.
transition probability에다가 첫번째 input 단어가 j상태가 나타났을 때 첫번째 observation이 나타날 확률을 곱해주는 것
o1은 3, o2는 1, o3는 3이다. 인풋이 세 개인데, 이 세 개에 대해서 가능한 모든 시퀀스의 확률값을 다 더해주고 싶은 것이다. 이 그림 전체가 알파 매트릭스라고 생각하자.
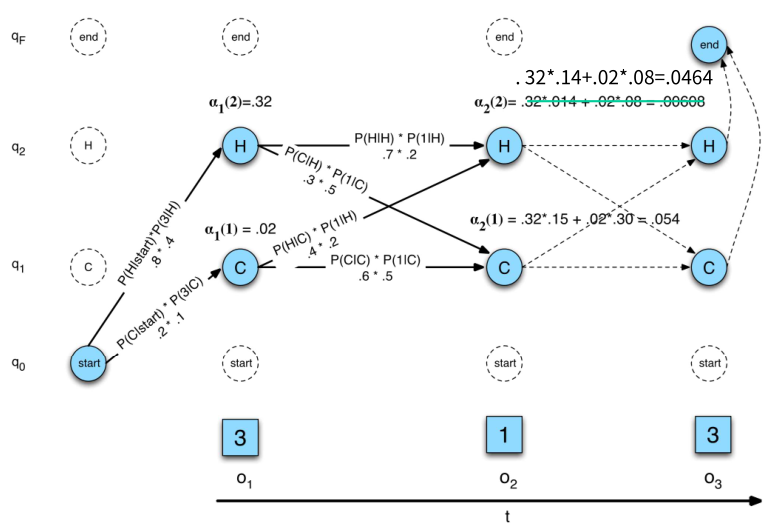
- q0(start), q1, q2, qF(final) 에는 모든 가능한 상태가 들어온다. COLD아니면 HOT. 실제 매트릭스는 q1, q2밖에 없다.
- start에서 HOT으로 갈 확률, HOT일때 3이 될 확률을 구한다.
- 0.2 * 0.1을 계산한 값이 a1(1)에 저장된다. 똑같이 a1(2)도 저장 ⇒ 3이 나타날 확률값이 계산됨
- 그 다음, a1(1), a1(2) 각각을 start state인 것 처럼 계산한다.
- 쭉쭉 채워서 매트릭스를 다 계산한 다음은 다 합해준다 → 3 1 3이 나타날 모든 확률값을 더해준 값
⇒ 일반화 : t번째 인풋이 왔을 때 어떤 상태인지 우리가 모른다. j번째 상태가 될 확률을 알파 t의 (j)라고 한다.
Forward 알고리즘 일반화 (N은 상태의 개수)
- 모든 품사 시퀀스를 가정했을 때 가능한
디코딩
- 가장 확률 값이 높은 하나의 시퀀스만 찾는 것
- observation 시퀀스 3 1 3이 나타났을 때 이 observation 시퀀스에 잘 맞는 최적의 상태 시퀀스를 찾아내는 것이다.
- 각각의 hidden 상태 시퀀스는 다양하게 나오는데 아까는 sum을 했지만, sorting을 해서 가장 높은 것을 선택한다.P(3 1 3 | HHC)
- …
- P(3 1 3 | HHH)
- 하지만 여기서 문제는 이 개수가 Nt개인데, 다 계산해서 sorting한다는 건 포워딩 알고리즘과 똑같다. = Viterbi 알고리즘
- 이것은 또한 동적 프로그래밍 알고리즘이기도 하다.
Viterbi 알고리즘
- 최상의 상태 시퀀스와 함께 observation 시퀀스의 결합 확률을 계산한다.
- 위에서 했던 알파tj와 똑같지만, sum이 아닌 max!
- Initialization : bt라는 매트릭스 (back point, 모두 0으로 채워준다. 이전 상태가 모두 0 상태이기 때문이다. 바로 이전 인덱스 값만 담아놓은 매트릭스다. 추적하기 위해 담아 놓음)
- Recursion : max! 앞에서 온 모든 것을 더하지 않고, 그 중 가장 큰 값을 뽑는다.
⇒ i부터 N중에 argmax가 되는 i값을 저장하라! (확률값 저장X, i값 저장. 교재에 식이 좀 이상함)
- Termination : final에 들어가는 것 중 가장 베스트 스코어가 나온다. argmax가 되는 그때의 i값이 qT에 들어간다.
Viterbi backtrace : 역추적
HMM(은닉 마르코프 모델)
- ★★시퀀스에 대한 확률적 생성 모델 (수학적으로 깔끔하게 정리되었고, 설명할 수 있다는 뜻임)
- 뉴럴네트워크와는 다른 모델이다. 뉴럴 네트워크는 확률적 모델이 아니기 때문이다.
- 숨겨져있는 상태를 찾아내는 것을 설명한다.
- 모델이 있을 수 있는 숨겨진 상태의 기본 세트를 가정 (예 : 품사)
- 시간 경과에 따른 상태 간의 확률적 전환을 가정(예: 시퀀스가 생성될 때 POS에서 다른 POS로 전환)
- 상태에서 토큰의 확률적 생성을 가정(예: 각 POS에 대해 생성된 단어)
HMM 학습 방식
- 지도학습 : 모든 훈련 시퀀스는 완전히 레이블이 지정된다.(정답이 태깅되어 있는)
- 비지도 학습 : 모든 훈련 시퀀스는 레이블이 지정되지 않는다.(걍 코퍼스임) 그러나 일반적으로는 태그의 수, 즉 상태가 몇 개인지를 알고 있음
- 반지도 학습 : 일부 훈련 시퀀스는 레이블이 지정되고 대부분은 레이블이 지정되지 않는다.
지도 HMM 훈련
- 전부 레이블링이 되어있으니, 우리는 카운트만 하면 된다.
- 훈련 시퀀스를 생성한 기본 상태 시퀀스로 레이블이 지정(태그 지정)된 경우, 매개변수 λ = {A, B}를 모두 직접 추정할 수 있다.
- 아래 그림에서 화살표는 모두 transition probability 이다. state는 항아리. 하나의 인풋에 대해 여러개의 상태에 대한 observation probability가 담긴다고 해서 항아리 모양.

지도학습 파라미터 추정
- transition probability(aij)는 어떻게 구하느냐? qi에서 qj로 가는.
- 일단 유니그램(qi번째의 상태)을 다 구한다. Si(i번째 품사) 어떤 특정 품사가 동사로 나타난 횟수를 구하고 그 단어가 동사로 나타났을 때, 그 다음 단어가 명사로 나타난 횟수 (예를 들어 j가 명사라고 했을 때)
- 레이블이 지정된 데이터에서 태그/단어 동시 발생 통계를 기반으로 관찰 확률을 추정합니다.
⇒ 특정 단어가 어떤 품사로 나타났을 때 그 단어가 vk로 나타날 확률
book이라는 단어가 명사로 나타날 확률인데, 거꾸로 하는 것이다. 명사가 나타났을 때 book이 나타날 확률을 구하는 것이다.⇒ bj(k) = j번째 품사가 k번째 단어로 나타날 확률- 훈련 데이터가 희소한 경우(sparse 데이터인 경우) 적절한 평활화(smoothing)를 사용한다. 0이 나오면 골치아프기 때문^^
= P( Book(vk) | noun(sj,상태) ) book이라는 단어가 명사로 사용된 횟수를 카운트하는 것이다.
HMM Taggers를 학습, 사용
- 품사가 붙어있는 코퍼스에서 HMM을 만들 수 있다. A,B를 카운트해서 찾을 수 있기 때문. 만들어내면 학습을 했다고 말할 수 있다. 새로운 데이터가 들어오면 그 모델을 가지고 품사를 매길 수 있다. 비터비 알고리즘 이용
- 가장 그럴듯한 태그 시퀀스를 예측한다. (단어열이 나타났을 때, 그 단어에 대해 가장 최적의 품사를 찾아내는 것)
Tagger 평가
- 트레이닝 데이터를 두 세개로 나눠서 (트레이닝 세트, 디벨롭먼 세트, 테스트 세트)
- 파라미터 값 튜닝 (성능에 따라 매개변수 조정 가능)
- 모델이 만들어지면 테스트 세트로 테스트를 한다.
- 일반적으로 측정 태그 정확도, 올바르게 태그가 지정된 토큰의 비율만 봄. 많이 맞을 수록 좋음
- HMM 포함한 최신 POC 태거의 정확도(accuracy)는 96-97%이다. 일반적으로 인간 수준과 일치한다.
Unsupervised maximum Likelihood Training
- 정답이 없고 시퀀스만 보여준 후 모델을 만들고, 모델에 넣어주면 맞춘다. (품사가 매겨지지 않은 문장만 쫙 가지고 오는 것임)
Maximum Likelihood Training
- 관찰 시퀀스 O가 주어지면 주어진 모델에 대해 이 데이터가 이 모델에서 생성될 확률(즉, P(O| λ))을 최대화하는 매개변수 집합 λ는 무엇인지.
⇒ O(코퍼스)를 주고 확률값을 최대로 하는 람다를 찾아내는(학습하는) 것이다. 모델을 만들었을 때 실제로는 Maximize하려고 하는데, 글로벌 맥시멈은 잘 못찾는다. 로컬 맥시멈은 잘 찾아감.
- HMM 모델을 훈련하고 훈련 데이터 세트에서 매개변수를 적절하게 유도하는 데 사용된다.
- 모델에서 생성된 주석 없는 관찰 시퀀스(또는 시퀀스 세트)만 있으면 된다. 관찰 시퀀스에 대한 올바른 상태 시퀀스를 알 필요가 없다.
HMM: Maximum Likelihood Training Efficient Solution
- P(O| λ)를 진정으로 최대화하는 매개변수 λ를 찾는 효율적인 알고리즘은 없다.
- 그러나 반복적인 재추정을 사용하여 EM(Expectation Maximization)이라고 하는 표준 통계 절차 버전인 Baum-Welch 알고리즘(a.k.a. forward-backward)은 P(O| λ)를 로컬 미니마이즈 할 수 있다.
- 실제로 EM은 많은 경우 훈련 데이터에 잘 맞는 좋은 파라미터 세트를 찾을 수 있다.
EM Algorithm
- 비지도 데이터로부터 확률적 범주화 모델을 학습하기 위한 반복적 방법
- 처음에는 범주에 대한 예의 무작위 할당을 가정한다. ⇒ 엉터리여도 노상관, 일단 랜덤하게 매겨주고 시작하는 것. 일단 엉터리라도 매겨져있으니 지도학습이 가능해진다.
- 무작위로 레이블이 지정된 이 데이터에서 모델 파라미터(세타라고 되어있는데 람다 얘기하는 것임 A,B)(통계쪽에서는 람다보다 세타를 더 많이 쓴다^^)를 추정하여 초기 확률 모델을 학습한다.
- 초기 확률값을 학습한 후 이 파라미터 값이 더이상 변하지 않을 때까지 (=convergence할 때까지) 아래 두 단계 반복(
- Expectation (E-step) : 기본적으로 계산 후 커런트 학습된 모델을 가지고 그 이그잼플들을 모두 re-labeling한다. 랜덤하게 이니셜라이즈드 한 걸 가지고 이니셜 모델을 만든다. (이니셜HMM) 그걸 가지고 다시 Expectation을 한다.(=초기데이터(하나도 태깅되지않은)를 일일히 다 한 번 품사를 매겨본다.)
- Maximization (M-step) : 처음에 랜덤하게 이니셜라이즈드된 데이터로부터 만든 hmm가지고 전체 코퍼스를 새로 태깅한다.(=Expectation) 이걸 가지고 다시 HMM을 만들어낸다.(=Maximization)
- ⇒ 확률적으로 다시 레이블이 지정된 데이터에서 모델 매개변수를 다시 추정한다.
EM
- Initialize : 레이블이 지정되지 않은 데이터에 임의의 확률 레이블 할당(⇒ 랜덤하게 카테고리를 정해준다. 당연히 틀린 정답이지만 일단 카테고리에 태그가 다 붙었기 때문에 학습이 가능해짐)→ 확률적 학습자에게 소프트 레이블 훈련 데이터 제공→ E단계 : 훈련된 분류기를 사용하여 레이블이 지정되지 않은 데이터에 레이블 재지정
→ M단계 : 레이블이 재지정된 데이터에 대해 분류기를 다시 학습시킨다. 레이블이 지정되지 않은 데이터의 확률 레이블이 수렴될 때까지 EM을 반복한다.
→ 확률적 분류기 생성(성능 똥망)
Sketch of Baum-Welch (EM) Algorithm for Training HMMs
- N개의 state를 가진 HMM을 가정한다.
- 매개변수 λ=(A,B)를 무작위로 설정(legal distribution : 다 더한 확률값이 1이 되도록 한다)
- 더이상 λ가 변경되지 않을 때까지 E단계와 M을 변경 시킴. 완전히 안 바뀌지는 않지만, 일정 수준 이상으로 떨어지면 중단 시킨다.
- E 단계: Forward/Backward 절차를 사용하여 훈련 데이터를 생성하기 위한 다양한 가능한 상태 시퀀스의 확률을 결정합니다. 태깅을 새로 해주는 작업
- M 단계: 태깅된 걸 가지고 와서 λ값을 카운팅하는 것
EM 속성
- 각 반복은 데이터의 확률값을 높이는 방식(개런티 해준다)으로 매개변수를 변경한다.
- Anytime알고리즘 : 적당할 때 언제든 중단할 수 있다.
- local 최대값으로 수렴할 수 있다.
반지도학습
- EM알고리즘은 레이블이 지정된 데이터와 레이블이 지정되지않은 데이터를 혼합하여 훈련한다.
- EM은 기본적으로 인스턴스의 확률적(소프트) 라벨링을 예측한 다음 이러한 예측된 라벨에 대한 지도 학습을 사용하여 반복적으로 재교육한다(self training)
- EM은 지도학습 데이터를 활용할 수도 있다.
1) 레이블이 지정된 데이터에 지도 학습을 사용하여 매개변수를 초기화한다(임의로 초기화하는 대신).
- 예시
2) 반복학습 동안 이러한 예제에 대해 소프트 레이블을 예측하는 대신, 지도학습 데이터에 대해 알려진 레이블을 사용한다.

사람 손으로 정답을 매긴 gold data에 기계학습을 통해 태깅된 데이터를 추가해 학습한다.
그렇게해서 만든 데이터를 가지고 다시 리-레이블링한다. 레이블이 지정되지 않은 데이터의 확률 레이블이 수렴될 때까지 반복을 계속 재훈련한다.- Semi-Supervised 결과
- Semi-Supervised 학습을 하는 이유 : 정답이 태깅된 데이터가 충분히 많이 있으면 그냥 지도학습을 하면 된다. 하지만! 레이블이 지정된 데이터의 양이 매우 적고 레이블이 없는 데이터의 양이 많을 때, 레이블이 없는 데이터를 추가로 사용하면 지도 학습의 성능을 향상 시킬 수 있다.
- 적절한 모델을 학습하기에 레이블이 지정된 데이터가 충분하고 비지도 학습이 원하는 레이블과 호환되지 않는 레이블을 생성하는 경향이 있는 경우, 성능이 저하될 수 있다. (품사를 태깅할때, 우리는 명사냐 동사냐만 태깅해줬음 좋겠는데 얘가 하다보니까 시맨틱 의미까지 있는 레이블로 학습해버림. 동사는 동사인데 먹는 동사라든지, 애니메이트 noun이라든지..)→ 비지도 학습은 순수한 구문 레이블(예: 동사, 명사)보다 데이터 예측에 더 나은 의미 레이블(예: 동사, 명사 애니메이션)을 학습하는 경향이 있기 때문에 준지도 POS 태깅에 대해 부정적인 결과가 있을 수 있다.
- 결론
- POS 태깅은 가장 낮은 수준(가장 기본적으로 해야하는)의 구문 분석이다.
- 이는 정보 추출, 구문 청크, 의미 역할 레이블 지정 및 생물 정보학에도 적용되는 collective 분류 작업인 시퀀스 레이블링이다. (다 똑같은 방식의 HMM 모델을 사용할 수 있다. BUT, state는 다르겠죠)
- HMM은 전 세계적으로 가장 확률적인 레이블 시퀀스를 효율적으로 계산하고 지도, 비지도 및 반지도학습을 지원하는 서열 라벨링을 위한 표준 생성 확률 모델이다.
'🤖 Education > 2021석사과정' 카테고리의 다른 글
| [자연어처리] 8. Sequence labeling and HMM part 3 (0) | 2023.08.25 |
|---|---|
| [자연어처리] 6. Sequence labeling and HMM part 1 (0) | 2023.08.18 |
| [자연어처리] 5. N-gram part2 (0) | 2023.08.15 |
| [자연어처리] 4.Grammars and Parsing part2 (0) | 2023.08.14 |
| [자연어처리] 3. Grammars and Parsing part1 (0) | 2023.07.25 |